【状態空間モデル入門】ローカルレベルモデル python スクラッチ実装！

【はじめに】状態空間モデルとは？

統計や時系列分析に興味を持っている方なら、状態空間モデルという言葉を聞いたことがあるかもしれません。これを使えば、観測されるデータの裏に潜む「真の状態」を推定することができ、特に時系列データの予測やフィルタリングにおいて非常に強力な手法です。

今回の記事では、その中でも基本的な「ローカルレベルモデル」に焦点を当て、Pythonを使ってスクラッチで実装する方法をご紹介します。このモデルは、データのトレンドや変動をシンプルかつ効果的に表現できるため、入門者にも最適なテーマです。

なぜローカルレベルモデルを学ぶべきか？

状態空間モデルにはさまざまなバリエーションがありますが、ローカルレベルモデルはその中でも基礎的な構造を持つため、他の複雑なモデルを学ぶ前のステップとして非常に重要です。このモデルを理解することで、より高度な時系列分析へのステップアップがスムーズになるでしょう。

さらに、ローカルレベルモデルは実際のデータ解析にも応用されており、経済データや気象データ、マーケティングデータなど、幅広い分野で利用されています。そのため、基礎をしっかり押さえておくことで、将来的に実務での活用が期待できます。

数式表現

ローカルレベルモデルは以下のような観測方程式と状態方程式を持ちます。

観測方程式

\[ y_t = \alpha_t + \epsilon_t , \, \, \epsilon_t \sim N(0, \sigma_{\epsilon} ) \]

状態方程式

\[ \alpha_{t+1} = \alpha_{t} + \eta_t , \, \, \eta_t \sim N(0, \sigma_{\eta} ) \]

\[ \alpha_1 \sim N(0, P_1 ) \]

\( y_t \) : 時点\( t \)の観測値
\( \alpha_t \) : 時点\( t \)の状態
\( \sigma_{\epsilon} \) : 観測値の分散
\( \sigma_{\eta} \) : 状態の分散
\( \alpha_1 \) : \( \alpha \) の初期値
\( P_1 \) : \( \alpha \) の分散の初期値

以上の構造を用いて入手できるデータ\( y_t \)から状態 \( \alpha_t \)を推定することを目指します。

いざ、実装！ ~ローカルレベルモデル~

まずは使用するライブラリをインポートします

import requests
import io
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

今回はAirPassengersのデータを使用します

url = "https://www.analyticsvidhya.com/wp-content/uploads/2016/02/AirPassengers.csv"
stream = requests.get(url).content
df_content = pd.read_csv(io.StringIO(stream.decode('utf-8')))
df_content['Month'] = pd.to_datetime(df_content['Month'], infer_datetime_format=True)
y = pd.Series(df_content["#Passengers"].values, index=df_content['Month'])
y = y.astype('f')
y.plot()

観測値は以下のような時系列になっています

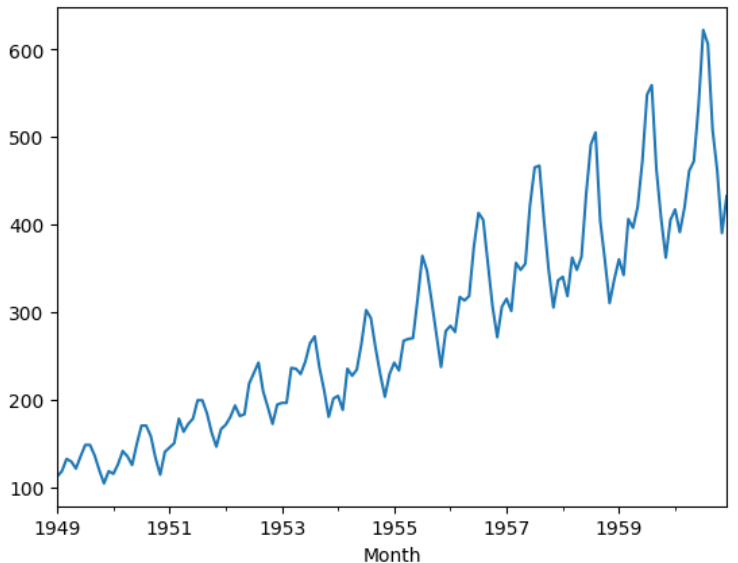
kfLocallevelという状態を推定する関数を作ります。

一期先予測→フィルタリングを繰り返すことで状態が推定できます。

# 1期先予測とフィルタリング

def kfLocallevel(y, mu_pre, P_pre, sigma_w, sigma_v) :
　　"""
    y : 観測値
    mu_pre : 状態
    P_pre : 状態推定誤差
    sigma_w : 過程誤差
    sigma_v : 観測誤差
    """
    # step1 予測
    mu_forecast = mu_pre
    P_forecast = P_pre + sigma_w
    y_forecast = mu_forecast
    F = P_forecast + sigma_v

    # step2 フィルタリング
    K = P_forecast / F
    y_resid  = y - y_forecast
    mu_filter = mu_forecast + K * y_resid
    P_filter = P_forecast * (1-K)

    # 結果の格納
    res = np.array([mu_filter,P_filter,y_resid, F])

    return res

AirPassengers観測値の状態を上のkfLocallevel関数で推定していきます

n = len(y)
mu_filter = np.zeros(n+1)
P_filter = np.append(np.array(10e7), np.zeros(n))
y_resid = np.zeros(n)
F = np.zeros(n)
K = np.zeros(n)

sigma_w = 10000
sigma_v = 1000

for i in range(n):
  res = kfLocallevel(y = y[i],
                    mu_pre = mu_filter[i],
                    P_pre = P_filter[i],
                    sigma_w = sigma_w,
                    sigma_v = sigma_v)
  mu_filter[i+1] = res[0]
  P_filter[i+1] = res[1]
  y_resid[i] = res[2]
  F[i] = res[3]

カルマンフィルタを用いて観測値から状態の推定をしたのでひとまず結果を以下に示します

plt.plot(mu_filter[1:], label = 'filter')
plt.plot(np.array(y), label = 'y')

plt.legend()
plt.show()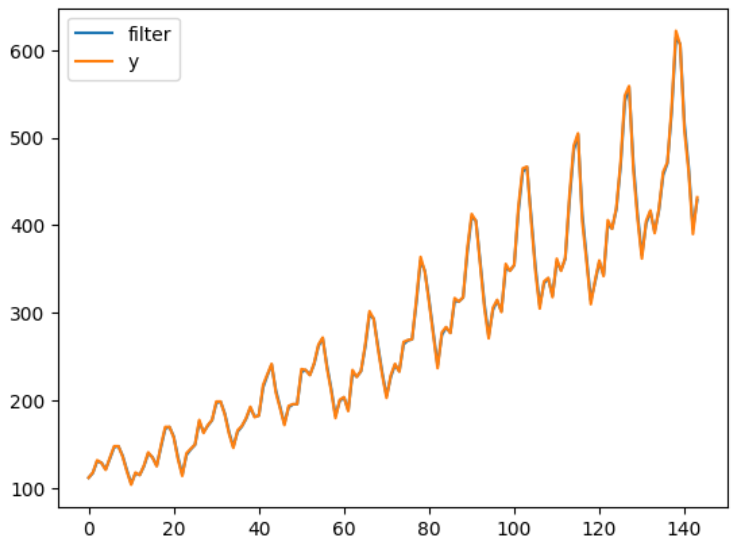

sigma_w（過程誤差）をsigma_v（観測誤差）より大きく設定したことから状態が観測値にかなり寄って推定されていることがわかります。過程誤差と観測誤差の大小を逆転して推定すると以下のような結果になります

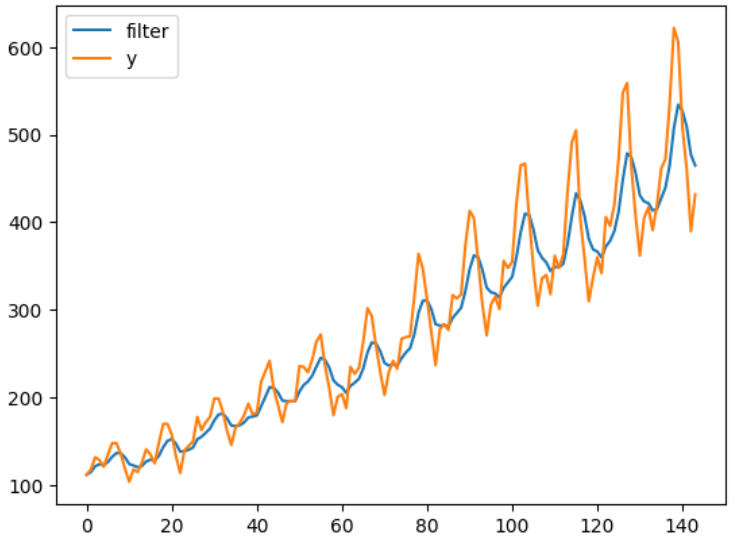
直感的な説明をすると、過程誤差と観測誤差それぞれは信頼の程度を表していると考えると良いのかなと思います。観測誤差が大きいと言うことは観測値があまり信用ならないということでカルマンフィルタの際に状態推定値を観測値近くに修正しないということです。