【はじめに】ポケカと統計学の意外な関係?
ポケモンカード(ポケカ)は戦略性の高いゲームですが、その中には確率に基づくアクションが含まれます。特に「ウラが出るまでコインを投げる」という試行は、デッキ構築やプレイングに大きな影響を与える可能性があります。しかし、この試行が本当に強力な仙術なのか、直感だけで判断するのは難しいところです。
この記事では、統計学の知識を活かし、この「ウラが出るまでコインを投げる」試行が幾何分布に従うことを説明します。さらに、Pythonを使ってその結果をシミュレーションし、実際にこの戦術がデッキに組み込むほど強力なのかを検証します。ポケカプレイヤーの方はもちろん、統計に興味がある方にも楽しんでいただける内容です!
【幾何分布とは?】コインを投げる試行の背景
まずは幾何分布について簡単に解説しましょう。幾何分布とは、何回目で始めて「成功」が起こるかを表す確率分布です。この場合の「成功」はコインの「ウラ」が出ることに相当します。
ポケカのゲーム内では、「ウラが出るまでコインを投げる」というアクションがありますが、この試行はランダム性を含むため、統計学的にはコインが「ウラ」になるまでに何回「オモテ」が出るかを幾何分布を使ってモデル化することができます。
幾何分布の確率関数は次のように表されます:
\[ P(X = k) = q^kp \]
\( q \):オモテが出る確率 \( (q=1-p) \)
\( p \):ウラが出る確率
\( k \) : 「ウラが出るまでコインを投げた回数」
ポケカの場合、コインの表裏が均等であれば\( p=0.5 \)です。
【実装】Pythonで「ウラが出るまでコインを投げる」をシミュレーション
次に、この幾何分布を使って、pythonでシミュレーションを行います。シミュレーションによって、実際にどのくらいの回数で「ウラ」が出るのか、そしてこの戦術がどの程度強力なのかを検証します。
まず、必要なライブラリをインストールし、シミュレーションを行うコードを書いてみましょう。
import numpy as np
import matplotlib.pyplot as plt
# 試行回数
n = 10000
p = 0.5 # ウラが出る確率
# 幾何分布に従う乱数生成(1回の試行ごとの投げた回数)
trial = np.random.geometric(p, n)
# 平均回数を計算
mu = np.mean(trial)
# 結果のプロット
plt.hist(trial, bins=np.arange(1, 15), density=True, alpha=0.75, color='b', rwidth=0.9)
plt.title("ウラが出るまでのコイン投げ回数の分布(幾何分布)")
plt.xlabel("コインを投げた回数")
plt.ylabel("確率")
plt.show()
print(f"ウラが出るまでにかかった平均回数: {mu:.2f}")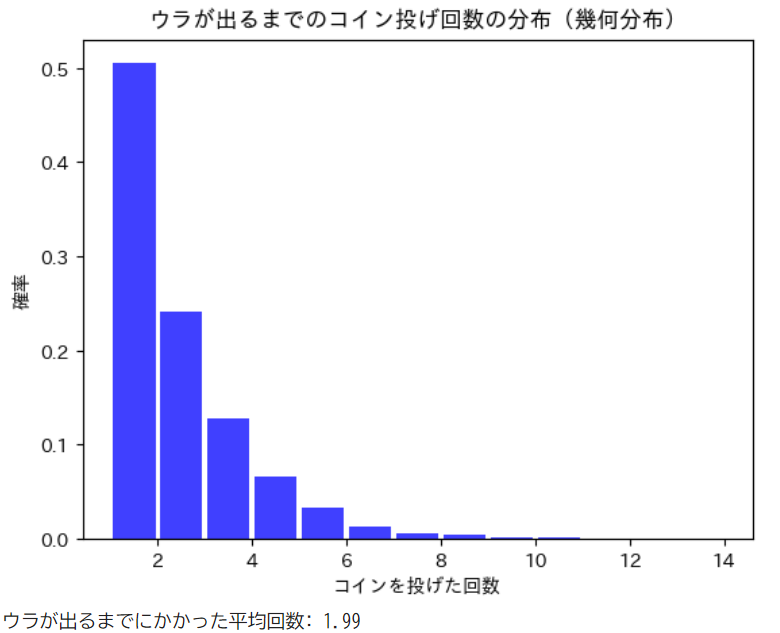
幾何分布の期待値は\( \frac{1}{p} \) なのでシミュレーションと同じ結果になりますね。
また、ウラが出る確率を減らすことでどの程度期待値が上昇するのかを見てみます。
# ウラが出る確率
p = np.arange(0.1, 0.55, 0.05)
# 幾何分布の期待値
mu = 1 / p
# グラフの描画
plt.plot(p, mu, marker='o', color='b', linestyle='-', label='期待値')
plt.title('ウラが出る確率と期待値の関係')
plt.xlabel('ウラが出る確率 (p)')
plt.ylabel('期待値 (mu)')
plt.grid(True)
plt.legend()
plt.gca().invert_xaxis() # 横軸を降順に設定
plt.show()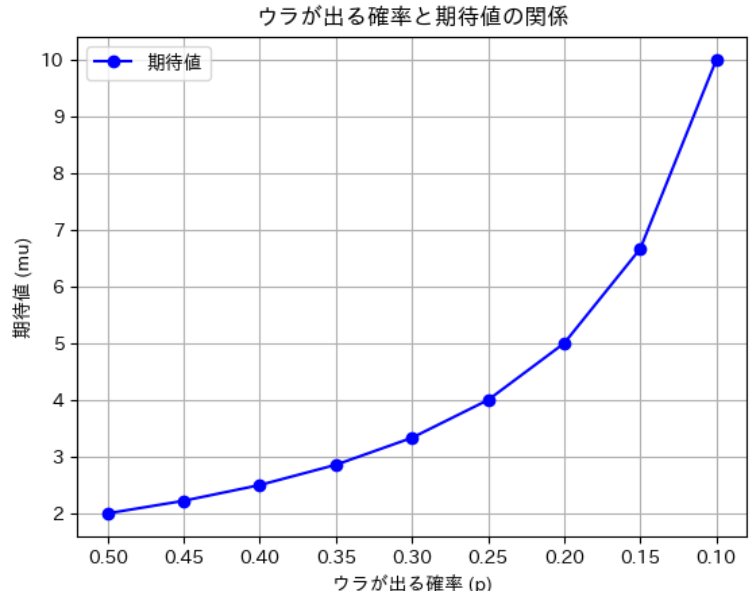
ウラが出る確率を0.5から0.1にする(オモテを90%の割合で出す)ことができれば10回試行できます。
もし特訓でオモテを70%で出すことができるようになれば3.3回試行できる(オモテを約2回出せる)ことがわかります。
【結果と考察】この戦術はデッキに組み込むべき?
シミュレーションや幾何分布の期待値から「ウラが出るまでコインを投げる」回数は約2回となることがわかります。幾何分布に従うため、1回でウラが出る場合もありますが、3回、4回とコインを投げることになるケースも珍しくありません。
強さのポイント
この戦術は、運に頼る側面が強く、1ターンで決定的な状況を作りたい場合にはリスクが高いです。しかし、運が味方すれば大きなアドバンテージを得る可能性もあります。試行が失敗(ウラが出る)しても大きなペナルティがない場合や次のターンでリカバリー可能な状況であれば、リスクを取りつつ戦略的に活用できるでしょう
【まとめ】統計的に見た「コインを投げる戦術」の可能性
統計的な分析を通じて、「ウラが出るまでコインを投げる」という試行は運に依存しつつも期待値的には1回オモテが出るということがわかりました(オモテが出せるように特訓すれば期待値を上昇させることもできますが笑)。幾何分布に従うこの試行は運と戦略のバランスに影響します。
ポケカのデッキ構築やプレイングの際には、こうしたランダム性を考慮するとより深い思考ができると思います。確率や戦略についていろいろ書きましたが、コイン投げによるハラハラを楽しんでいきましょう!


コメント